Use the Get in touch link if you’re interested in supporting this project.
Qualifying teammate battles seem to be of great interest to the current F1 community. While I’m a firm believer that Sundays matter far more than Saturdays, I can’t deny the growing importance of qualifying—especially with how tough overtaking has become with the latest generation of F1 cars. Track position is king, and starting ahead often means staying ahead. So while race day is where the points are handed out, Saturdays are playing a bigger role than ever in shaping the final results.
No, ChatGPT didn’t write this article. Yes, there are some of us out there who use the em dash.
Analysis
Click to expand methodology
Methodology!
As with race pace, we can’t directly compare qualifying pace between races. Different tracks, lengths, and deltas make it tricky. To handle this, I standardized the data using a metric called symmetric percent difference. Without getting too technical, it’s a more robust way of calculating percent differences — hence why I chose it.
I calculated the symmetric percent difference for all qualifying sessions between teammates, keeping only the maximum session where both drivers participated. For example, if George Russell made it to Q3 but his teammate only reached Q2, I used the Q2 data for the comparison. If a driver couldn’t set a lap time in Q1 while their teammate did, I removed that session entirely. While this isn’t ideal, using equally comparable data points is crucial for a fair performance comparison. Negative symmetric percent difference values mean that a driver was faster than his teammate, while positive values mean that the driver was slower than his teammate. A difference of 0% means that both drivers were just as fast.
I calculated the values for each race for each team and plotted them as individual data points in the chart. I then calculated the median of these values for the season (so far) and displayed it the left side of the plot, next to the team logo. Smaller overall values represent that both teammates were more evenly matched during quali, while larger overall values show a greater gap between teammates.
Additionally, on the left-hand side of the chart next to the driver’s name, I also added the number of times a particular driver has been faster than his teammate in quali.
Finally, I added a gold-coloured diamond to show the median gap between teammates. This number will be equal to the overall value displayed on the left side of the plot, next to the team logo.
Issues!
One of the main issues when gathering data from multiple races is that the deltas will change depending on the length of each track. A delta of 0.1 seconds in a short track (say, 1:05 per lap) will be greater than a delta of 0.1 seconds in a long track such as Spa (~ 1:45).
One way we can standardize the data is by converting the deltas to percentages, but there is one big issue with this. The traditional way of calculating a percent difference is with the following formula:
$$ Percent\ difference = 100\times\frac{value1-value2}{value2} $$
The main problem is that this value is not symmetrical. This means that if I reverse the order of value 1 and value 2, the final percent difference will be different.
$$ Percent\ difference = 100\times\frac{80-90}{90}=-11.11\% $$ $$ Percent\ difference = 100\times\frac{90-80}{80}=12.5\% $$
You can see that the percentages are not reversible, even though in both cases we’ve changed the original value by 10 units.
One way we can solve this problem is by using the symmetric percent difference, which is calculated by using the following formula:
$$ Symmetric\ percent\ difference = 100\times\frac{value1-value2}{(value1+value2)/2} $$ This formula is reversible, meaning that regardless of the order of the values, we will get the same result. Because of this, I decided to use the symmetric percent difference formula as the basis for the analysis.
Quali delta between teammates
We’re already halfway into the season. With 12 races, and 2 sprints, we now have more representative results. Just as a reminder, this season, we have the anomaly of Lawson switching places with Tsunoda after just three races, which makes our usual analysis a little trickier. Additionally, Alpine have decided to replace Doohan with Colapinto after just 6 races. Normally, I’d just use the median as the key metric of interest since it’s more robust to outliers. However, in this case, the median might skew the average delta between Lawson and Verstappen.
To counter that, I’ve decided to include both the median and the mean qualifying deltas in this article. This approach might change in future posts, but for now, I think it gives us a more complete picture.
The results have now stabilized after 14 sessions, which means that at this point in time the mean is the most representative metric for most pairings.
Symmetric percent difference

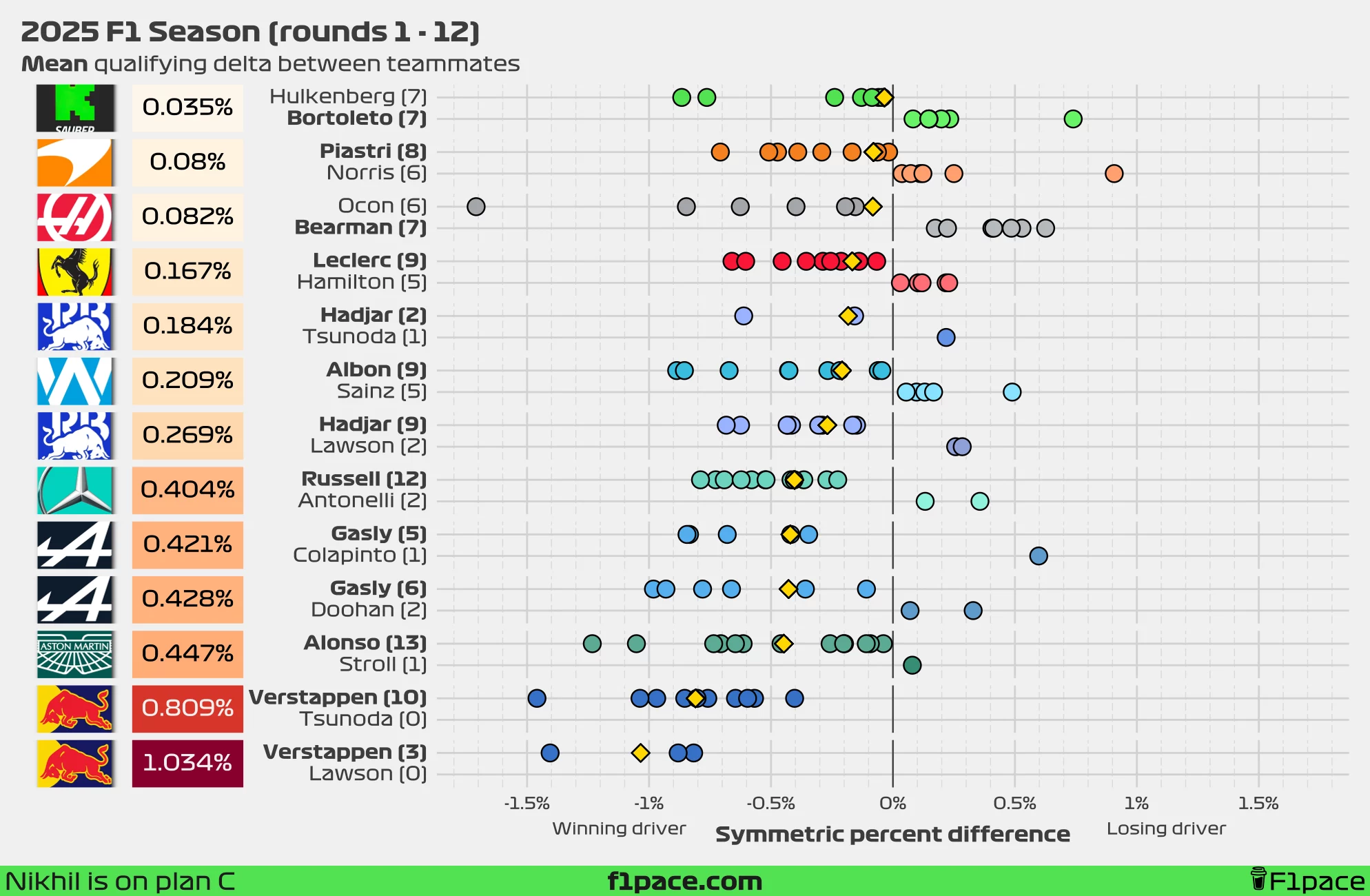
Looking at the median symmetric percent difference, the biggest gap between teammates remains at Red Bull Racing. Tsunoda continues to struggle and hasn’t made a Q3 appearance since the Miami GP, which was two months ago. At the latest British GP, he trailed Verstappen by 0.595%. Currently, Verstappen is beating Yuki Tsunoda by 0.781%, which is still slightly less than the median delta left by Lawson at 0.881%.
If we look at the mean symmetric percent difference instead, the largest gap shifts to Verstappen vs. Lawson, with Max ahead by an average of 1.034%. Yuki continues to reduce the gap to Max, but I doubt he’ll be satisfied with his recent performances. His current delta to Max stands at 0.809%, which is 80% more than the next largest gap—Alonso vs. Stroll.
At the other end of the spectrum, the smallest delta has fully shifted to Sauber. Bortoleto has taken the lead against Hulkenberg in quali, which is a great achievement for a rookie. Using the median, the gap is just 0.02%, while using the mean, it stands at 0.035%, both in favour of the Brazilian driver.
Delta in seconds
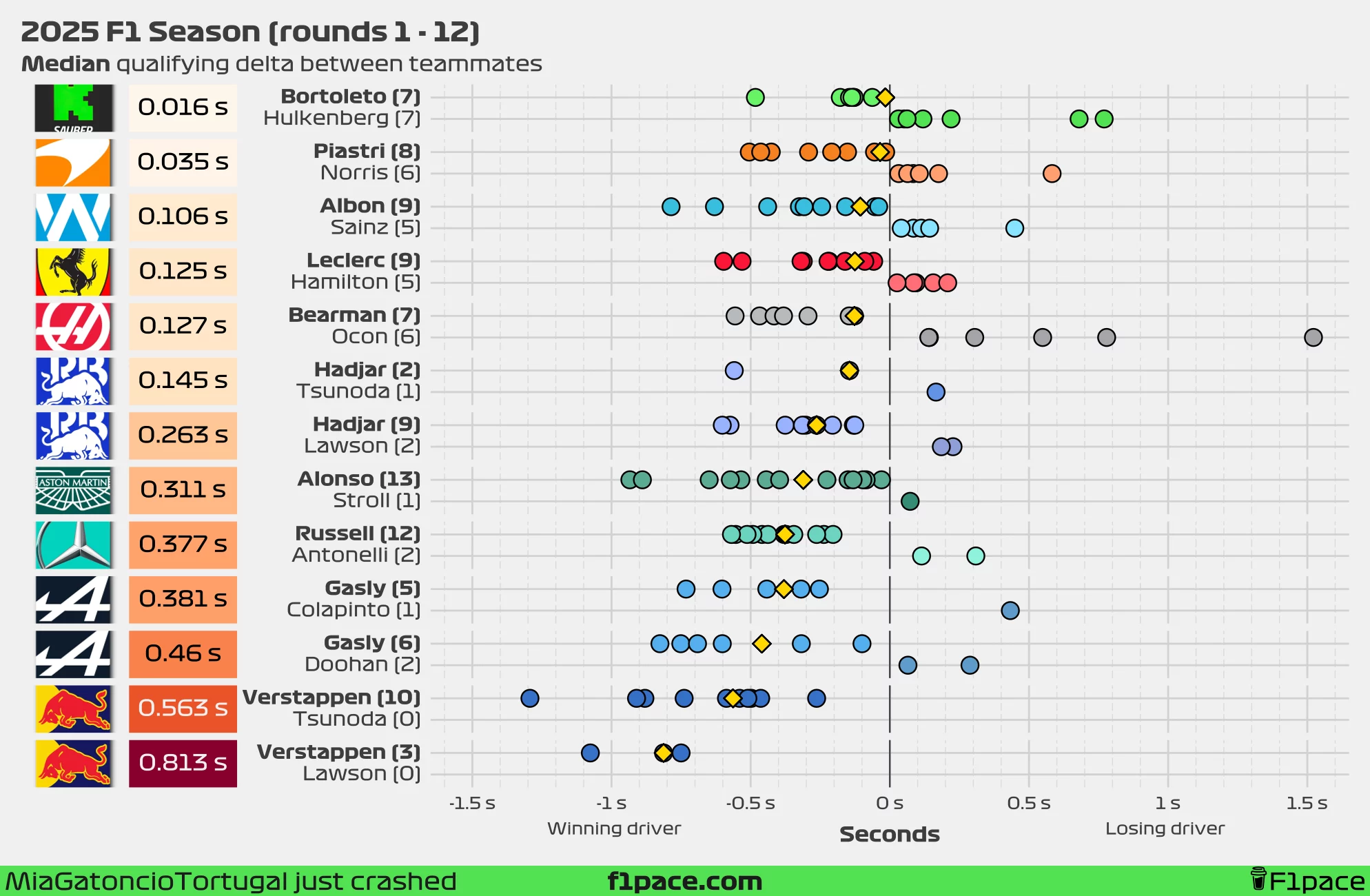

I will continue to include the analysis using seconds instead of the symmetric percent difference. I’m still firmly in the “symmetric percent difference is more representative” camp, but the difference between the two metrics is smaller than most people think—and time in seconds is a lot easier to interpret for most people.
Just as with the symmetric percent difference, the smallest gap is found at Sauber. Looking at the median delta, the gap is just 0.016 seconds in Bortoleto’s favo, while the smallest mean gap has Gabriel leading Nico by 0.048 seconds.
I think the biggest gap will remain at Red Bull for the rest of the season. I just don’t see how Tsunoda can close the gap enough to come close to any other pairing. As I mentioned, the delta between Max and Yuki has decreased, but that’s mostly due to the extreme gaps he had earlier in the season—Bahrain (0.879s), Saudi Arabia (0.91s), and Miami (0.739s). Tsunoda could still be getting deltas to Max of over half a second, and it would improve his overall relative performance. At the moment, Max Verstappen is ahead of Yuki Tsunoda by a median of 0.563 seconds and a mean of 0.668 seconds.
Qualifying stage appearances

If the text appears a bit too small, feel free to zoom in to see each individual bubble more clearly.
Click to expand explanation
I’ve often seen tables showing how many times drivers reached Q1, Q2, and Q3, but I’ve never been fully satisfied with them. Tables tend to have too much text while still missing key insights. To address this, I created a bubble chart.
Each bubble represents a driver’s qualifying or sprint qualifying appearance throughout the 2025 F1 season. The bubble’s size reflects the driver’s final qualifying position, with larger bubbles indicating better results. The actual position is displayed as a big number inside the bubble, and the colors indicate the qualifying session reached.
As of the 12th race of the 2025 season, most teammate pairings have been fairly evenly matched, with just a few notable exceptions. The first remains Aston Martin, where Alonso has reached Q3 six times, while his teammate, Lance Stroll, has managed it only twice. The second is at Alpine, with Gasly doing a great job in a struggling car. Pierre has qualified for Q3 on seven occasions, while Doohan and Colapinto combined have yet to make a single Q3 appearance. The third exception is, unsurprisingly, Red Bull Racing. So far, Max Verstappen has reached Q3 in all 14 possible sessions and is one of just three drivers to do so, along with Lando Norris and Oscar Piastri. Meanwhile, Lawson was eliminated in Q1 three times while racing for Red Bull. In Tsunoda’s case, his Q3 record continues to suffer, with just three appearances out of 11 outings for the team—putting his rate at 27.2%.
